Question

An ellipse has a center at the origin, a vertex along the minor axis at (0,-8), and a focus at (15,0). Which equation represents this ellipse?

Answer 1

We have been given that an ellipse has a center at the origin, a vertex along the minor axis at (0,-8), and a focus at (15,0). We are asked to find the equation for the ellipse.

The standard from an ellipse centered at origin with major axes at x-axis is
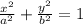`(x^2)/(a^2)+(y^2)/(b^2)=1`, where

a = Horizontal radius,

b = Vertical radius.

Since focus is at x-axis, so our ellipse will be a major horizontal axis.

Horizontal radius will be equal to distance from origin to point (15,0) that is
`a=15-0=15`

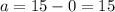
The vertical radius would be distance from origin to point (0,-8) that is:

`b=√((0-(-8)^2))=8`

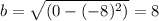
Upon substituting values of a and b in above equation, we will get:

`(x^2)/(15^2)+(y^2)/(8^2)=1`

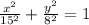
Therefore, our required equation would be
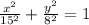`(x^2)/(15^2)+(y^2)/(8^2)=1`.