Question

Men’s heights are normally distributed with mean 69.5 inches and a standard deviation of 2.4 inches.

Women’s heights are normally distributed with mean 63.8 inches and a standard deviation of 2.6 inches

The Gulfstream 100 is an executive jet that seats six and it has a doorway height of 51.6 inches.

a. What percentage of adult men can fit through the door without bending?

b. what percentage of adult women can fit through the door without bending?

c. Does the door design with a height of 51.6 inches appear to be adequate? Why didn’t engineers design a larger door?

d. What doorway height would allow 60% of men to fit without bending?

Answer 1

a. The percentage of adult men that will fit through the door without bending is 0.

b. The percentage of adult women that will fit through the door without bending is 0.

c. No, it is not adequate. There must be another technical reasons to not use a larger door.

d. The doorway height that would allow 60% of men to fit without bending is 70.1 inches.

Explanation:

a. To fit throught the door, the height has to be under 51.6. To calculate this proportion, we have to calculate the z-score for X=51.6 for the distribution of men's height N(μ=69.5, σ=2.4).

We can calculate the z-score as:

`z=(X-\mu)/(\sigma)=(51.6-69.5)/(2.4)=(-17.9)/(2.4)=-7.4583`

`P(X<51.6)=P(z<-7.4583)=0`

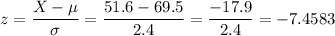
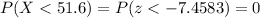
The percentage of adult men that will fit through the door without bending is 0.

b. To fit throught the door, the height has to be under 51.6. To calculate this proportion, we have to calculate the z-score for X=51.6 for the distribution of women's height N(μ=63.8, σ=2.6).

We can calculate the z-score as:

`z=(X-\mu)/(\sigma)=(51.6-63.8)/(2.6)=(-12.2)/(2.6)=-4.6923`

`P(X<51.6)=P(z<-4.6923)=0`

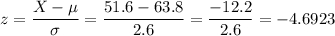
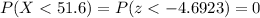
The percentage of adult women that will fit through the door without bending is 0.

c. No, it is not adequate. There must be another technical reasons to not use a larger door.

d. We can calculate this finding a z-value z1 for which P(z<z1)=0.60.

Looking in a standard normal distribution table, the value for z1 is z1=0.25335.

Then, transforming to our adult men's height distribution, we have:

`X=\mu+z\sigma=69.5+0.25335*2.4=69.5+0.6=70.1`

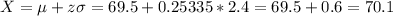
The doorway height that would allow 60% of men to fit without bending is 70.1 inches.