Question

What is the product of (3x-9) and 6x↑2-2x+5 Write your answer in standard form.

(a) Show your work.

(b) Is the product of (3x-9) and 6x↑2-2x+5 equal to the product of (9x-3) and 6x↑2-2x+5

Explain your answer.

Answer 1

a.
`18x^3 -60x^2 + 33x - 45`

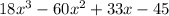
b. No

Explanation:

Given:

(3x-9) and
`6x^2-2x+5`

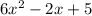
=> the production of them is:

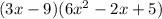`(3x-9)(6x^2-2x+5)` , we will use distributive law to solve this To do that. we first multiply
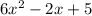`6x^2-2x+5` by 3x then by -9. This is done as follows

=
`3x (6x^2-2x+5) - 9(6x^2-2x+5)`
`= (3x * 6x^2-3x * 2x+3x *5) - (9* 6x^2-9* 2x+9* 5)\\\\= (18x^3 -6x^2+ 15x) - (54x^2 - 18x +45)`

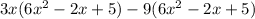
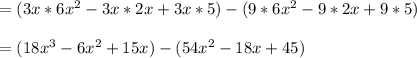
Then Open both brackets

=
`18x^3 -6x^2+ 15x -54x^2 + 18x -45`

After that, we group the same terms

=
`18x^3 -(6x^2 +54x^2)+ (15x + 18x) -45`

=
`18x^3 -60x^2 + 33x - 45`

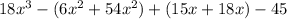
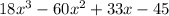
(b) Is the product of (3x-9) and
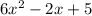`6x^2-2x+5` equal to the product of (9x-3) and
`6x^2-2x+5`

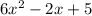
No, let find the product of (9x-3) and
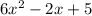`6x^2-2x+5` , we will use distributive law to solve this as the above example.

= (9x-3)
`(6x^2-2x+5)`

=
`9x (6x^2-2x+5) - 3(6x^2-2x+5)`

=
`(9x * 6x^2 - 9x * 2x + 9x *5) - (3* 6x^2 - 3 * 2x + 3* 5)`

=
`(54x^3 - 18x^2+ 45x) - (18x^2 - 6x +15)`

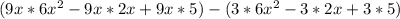
After that, we open the bracket to find the same terms

=
`54x^3 - 18x^2+ 45x -18x^2 + 6x -15`

=
`54x^3 - 18x^2 -18x^2 + 45x + 6x -15`

=
`54x^3 - 36x^2 + 51x -15`

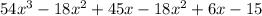
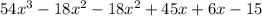
As you can see
`54x^3 - 36x^2 + 51x -15` ≠
`18x^3 -60x^2 + 33x - 45`

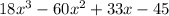
Hope it will find you well.