Answer:
Explanation:
a. Given
and
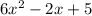
Required
Product
The solution is as follows
First, put both expression in different brackets
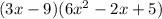
Expand
bracket by
To do that. we first multiply
by 3x then by -9. This is done as follows
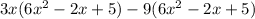
Now, we proceed to opening the bracket
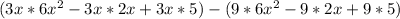
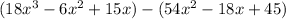
Open both brackets
Collect like terms
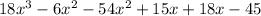
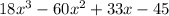
Hence, the product of
and
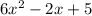is
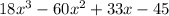
b. Given
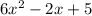
and
and
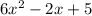
Required
Are their products equal?
To check if they are equal or not, we find the product of both and compare the solutions
We've already solved for
and
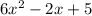in the (a) part of this exercise, so we move to the product of
and
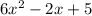
The solution is as follows
First, put both expression in different brackets
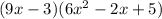
Expand
bracket by
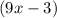
To do that. we first multiply
by 9x then by -3. This is done as follows
Now, we proceed to opening the bracket
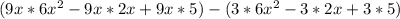
Open both brackets
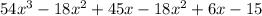
Collect like terms
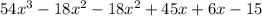
Now, we compare both answers
Is
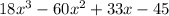
equal to
No, they're not.
Reason is that, for both expressions to be equal, we must have the same expression after expanding both of them