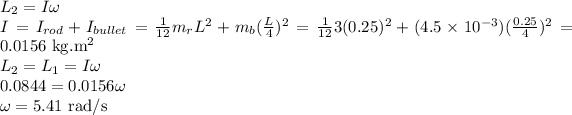Question

A bullet with a mass of 4.5 g is moving with a speed of 300 m/s (with respect to the ground) when it collides with a rod with a mass of 3 kg and a length of L = 0.25 m. The rod is initially at rest, in a vertical position, and pivots about an axis going through its center of mass which is located exactly halfway along the rod. The bullet imbeds itself in the rod at a distance L/4 from the pivot point. As a result, the bullet-rod system starts rotating together. What is the magnitude of the angular velocity (in rad/s) of the rotation (with respect to the ground) immediately after the collision? You may treat the bullet as a point particle.

Answer 1

ω = 5.41 rad/s

Step-by-step explanation:

Since the rod is rotating around its axis, angular momentum will play part in this question.

The conservation of angular momentum implies that

`L_1 = L_2`

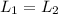
So, the initial angular momentum is

`L_1 = m_b v_b (L)/(4) = (4.5* 10^(-3)~{\rm kg})(300~{\rm m/s})((0.25)/(4)~{\rm m}) = 0.0844~{\rm kg.m^2/s}`

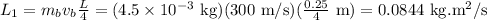
The final angular momentum includes the rod and the bullet together. So,

`L_2 = I\omega\\I = I_(rod) + I_(bullet) = (1)/(12)m_r L^2 + m_b((L)/(4))^2 = (1)/(12)3(0.25)^2 + (4.5* 10^(-3))((0.25)/(4))^2 = 0.0156~{\rm kg.m^2}\\L_2 = L_1 = I\omega\\0.0844 = 0.0156\omega\\\omega = 5.41~{\rm rad/s}`