Question

Explosive devices used in mining operations produce nearly circular craters when detonated. The radii of these craters are exponentially distributed with mean feet. Find the mean and variance of the areas produced by these explosive devices.

Answer 1

The mean and variance of the areas produced by these explosive devices are 200π and 2,00,000π² respectively.

Explanation:

The complete question is:

Explosive devices used in mining operations produce nearly circular craters when detonated. The radii of these craters are exponentially distributed with mean 10 feet. Find the mean and variance of the areas produced by these explosive devices.

Solution:

Let the random variable X be defined as the radius of a crater .

The random variable X follows an Exponential distribution with mean, μ = 10 feet.

Then the variance of X is:

`V(X)=(\mu)^(2) = 100\\`

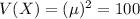
Then the area is:

`A=\pi X^(2)`

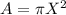
Compute the expected value of the area as follows:

`E(A)=E(\pi X^(2))\\=\pi* E(X^(2))\\=\pi* [V(X)+[E(X)]^(2)]\\=\pi* [100+100]\\=200\pi`

Compute the variance of the area as follows:

`V(A)=V(\pi X^(2))\\=\pi^(2)* V(X^(2))\\=\pi^(2)* [E(X^(4))-(E(X^(2)))^(2)]\\`

Compute the value of E (X⁴) as follows:

`E(X^(4)=\int\limits^(\infty)_(0) {(1)/(10)x^(4)e^(-x/10)} \, dx \\=10^(4)* 4!\\=240000`

The variance is:

`V(A)=\pi^(2)* [E(X^(4))-(E(X^(2)))^(2)]\\=\pi^(2)* [240000-200^(2)]\\=200000\pi^(2)`

Thus, the mean and variance of the areas produced by these explosive devices are 200π and 2,00,000π² respectively.