Answer:
(a) Margin of error = 0.0212.
(b) 95% confidence interval for the population proportion of people who believe in heaven is [0.82 , 0.86].
Explanation:
We are given that when 1146 subjects were asked, "Do you believe in heaven?" the proportion who answered yes was 0.84. The standard deviation of this point estimate is 0.01.
(a) Margin of error tells us that how many percentage points our results will differ from the true population proportion value.
Margin of error is given by =
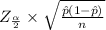
where,
 = point estimate or sample proportion = 0.84
= point estimate or sample proportion = 0.84
n = sample of subjects = 1146
 = significance level = 1 - 0.95 = 0.05
= significance level = 1 - 0.95 = 0.05
So, value of
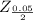 in z table is given as 1.96
in z table is given as 1.96
Hence, Margin of error =
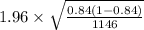 = 0.0212
= 0.0212
(b) Firstly, the pivotal quantity for 95% confidence interval for the population proportion is given by;
P.Q. =
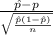 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of people who answered yes = 0.84
= sample proportion of people who answered yes = 0.84
n = sample of subjects = 1146
p = population proportion of people
Here for constructing 95% confidence interval we have used One-sample z proportion statistics.
So, 95% confidence interval for the population population, p is ;
P(-1.96 < N(0,1) < 1.96) = 0.95 {As the critical value of z at 2.5% level
of significance are -1.96 & 1.96}
P(-1.96 <
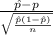 < 1.96) = 0.95
< 1.96) = 0.95
P(
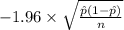 <
<
 <
<
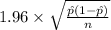 ) = 0.95
) = 0.95
P(
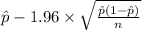 < p <
< p <
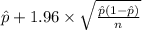 ) = 0.95
) = 0.95
95% confidence interval for p = [
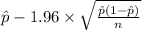 ,
,
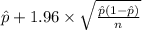 ]
]
= [
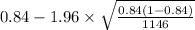 ,
,
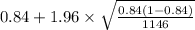 ]
]
= [0.82 , 0.0.86]
Therefore, 95% confidence interval for the population proportion of people who believe in heaven is [0.82 , 0.86].
Interpretation of above confidence interval is that we are 95% confident that the population proportion of people who believe in heaven will lie between 0.82 and 0.86.