Question

Find the area under the standard normal distribution curve between z=0 amd z=1.38

Answer 1

`P(0<z<1.38) = P(Z<1.38) -P(Z<0)`

And using the normal standard distribution table or excel we got:

`P(0<z<1.38) =0.916-0.5= 0.416`

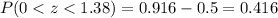
The excel code would be:

"=NORM.DIST(1.38,0,1,TRUE) -=NORM.DIST(0,0,1,TRUE)"

Explanation:

For this case we know that our random variable of interest is Z and the distribution is given by:

`Z \sim N(\mu =0 , \sigma =1)`

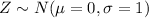
This distribution is an special case of the normal distribution.

And we want to find this probability:

`P(0<z<1.38)`

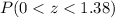
And we can find this probability with this difference and using the concept of cumulative distribution function for a continuous distribution:

`P(0<z<1.38) = P(Z<1.38) -P(Z<0)`

And using the normal standard distribution table or excel we got:

`P(0<z<1.38) =0.916-0.5= 0.416`

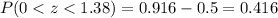
The excel code would be:

"=NORM.DIST(1.38,0,1,TRUE) -=NORM.DIST(0,0,1,TRUE)"