Question

Find the counterclockwise circulation and outward flux of the field Fequals7 xy Bold i plus 2 y squared Bold j around and over the boundary of the region C enclosed by the curves yequalsx squared and yequalsx in the first quadrant.

Answer 1

The counterclockwise circulation is
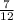`(7)/(12)` and the outward flux is
`(11)/(15)`

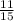
Explanation:

We are given the field
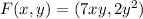`F(x,y) = (7xy,2y^2)`. A picture of the region and the path we are considering is attached. Recalll the following theorems.

Given a field of the form F(x,y)=(f(x,y),g(x,y) with f,g having continous partial derivates, C is a closed path counterclockwise oriented, R is the region enclosed by C and n is the normal vector pointing outwards of the path C. Then

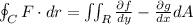`\oint_C F\cdot dr =\iint_R (\partial f)/(dy)- (\partial g)/(dx) dA`(this one calculates the counterclockwise circulation)

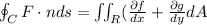`\oint_C F\cdot n ds =\iint_R ((\partial f)/(dx)+ (\partial g)/(dy) dA` (This one calculates the outward flux)

Then, recall that in our case f(x,y) = 7xy, g(x,y)=2y^2[/tex]. Then

`(\partial f)/(dx) = 7y,(\partial f)/(dy) = 7x`

`(\partial g)/(dx)=0, (\partial g)/(dy) = 4y`.

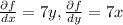
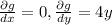Note that we just need to describe our region R. The region R lies between the parabola y=x^2 and the line y=x. Thus, one way to describe the region is as follows
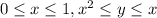`0\leq x \leq 1, x^2\leq y \leq x`. Then, using the previous results, we get that

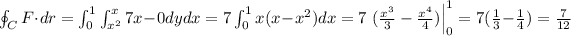`\oint_C F\cdot dr =\int_(0)^(1)\int_(x^2)^(x)7x-0dydx = 7\int_(0)^1x(x-x^2)dx = 7 \left.((x^3)/(3)-(x^4)/(4))\right|_(0)^1 = 7((1)/(3)-(1)/(4)) = (7)/(12)` (circulation)

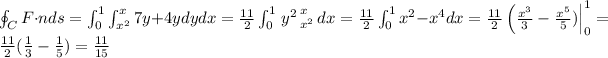`\oint_C F\cdot n ds=\int_(0)^(1)\int_(x^2)^(x)7y+4ydydx = (11)/(2)\int_(0)^1\left.y^2\right_(x^2)^(x)dx = (11)/(2)\int_(0)^(1)x^2-x^4 dx = (11)/(2)\left((x^3)/(3)-(x^5)/(5))\right|_(0)^(1)=(11)/(2)((1)/(3)-(1)/(5))=(11)/(15)`(flux)