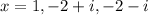Question

If f(x) = 2x^3 +6x^2+2x - 10 and f(1) = 0, then find all of the zeros of f(x) algebraically.

Answer 1

`\displaystyle x = 1, - 2 + i, -2 -i`

Explanation:

We are given that:

`\displaystyle f(x) = 2x^3 + 6x^2 + 2x - 10 \text{ and } f(1) = 0`

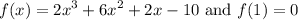
And we want to find all zeros of f algebraically.

Since f(1) = 0, then (x - 1) is a zero of f.

We can hence factor by synthetic division:

`\begin{table}[]\begin{tabular}{lllll}\multicolumn{1}l{1} & 2 & 6 & 2 & -10 \\\multicolumn{1}l{} & & 6 & 2 & 10 \\ \cline{2-5} & 2 & 8 & 10 & -10 \\ & & & & \end{tabular}\end{table}`
`\begin{tabular}{lllll}\multicolumn{1}l{1} & 2 & 6 & 2 & -10 \\\multicolumn{1}l{} & & 2 & 8 & 10 \\ \cline{2-5} & 2 & 8 & 10 & 0 \\ & & & & \end{tabular}`

Therefore:

`\displaystyle \begin{aligned} f(x) & = 2x^3 + 6x^2 + 2x- 10 \\ \\ & = (x-1)(2x^2 + 8x + 10) \\ \\ &= 2(x-1)(x^2 + 4x + 5)\end{aligned}`

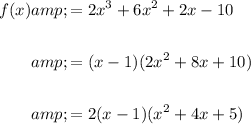
Therefore, by the Zero Product Property:

`\displaystyle x-1 = 0 \text{ or } x^2 +4x + 5 = 0`

From the quadratic formula:

`\displaystyle \begin{aligned}x & = (-b\pm√(b^2-4ac))/(2a) \\ \\ & = (-(4)\pm√((4)^2 - 4(1)(5)))/(2(1)) \\ \\ &= (-4\pm√(-4))/(2) \\ \\ &= (-4\pm 2i)/(2) \\ \\ & = -2\pm i \end{aligned}`

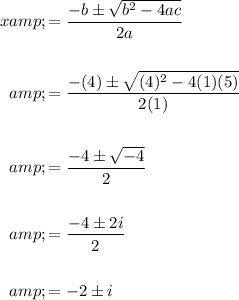
Therefore, all the zeros of f include:

`\displaystyle x = 1, - 2 + i, -2 -i`