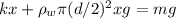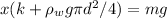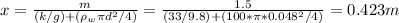Answer:
0.423m
Step-by-step explanation:
Conversion to metric unit
d = 4.8 cm = 0.048m
Let water density be
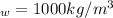
Let gravitational acceleration g = 9.8 m/s2
Let x (m) be the length that the spring is stretched in equilibrium, x is also the length of the cylinder that is submerged in water since originally at a non-stretching position, the cylinder barely touches the water surface.
Now that the system is in equilibrium, the spring force and buoyancy force must equal to the gravity force of the cylinder. We have the following force equation:
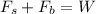
Where
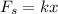 N is the spring force,
N is the spring force,
 is the buoyancy force, which equals to the weight
is the buoyancy force, which equals to the weight
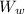 of the water displaced by the submerged portion of the cylinder, which is the product of water density
of the water displaced by the submerged portion of the cylinder, which is the product of water density
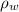 , submerged volume
, submerged volume
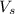 and gravitational constant g. W = mg is the weight of the metal cylinder.
and gravitational constant g. W = mg is the weight of the metal cylinder.
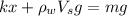
The submerged volume would be the product of cross-section area and the submerged length x
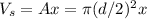
Plug that into our force equation and we have