Question

What is the least common denominator of the expression below

Answer 1

We must factor the denominators first. And to factor a quadratic equation, you need its roots.

We will use the fact that any quadratic equation with leading coefficient 1, i.e. in the form
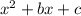`x^2+bx+c` has the following properties:

• The sum of the roots is
  `-b`
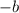
• The product of the roots is
  `c`

So, for the first denominator, we're looking at two numbers such that their sum is -4 and their product is -12. It's easy to find out that those numbers are 2 and -6.

Similarly, for the second denominator, we're looking at two numbers such that their sum is -7 and their product is 6. It's easy to find out that those numbers are -1 and -6.

So, you can rewrite the expression as follows:

`(x^2+6)/((x-2)(x+6))+(7x)/((x+1)(x+6))`

The least common denominator is formed by the factors of the two denominators, and you have to select repeating ones only once.

Answer 2

answer: B (x+6)

Explanation:

hello :

x²+7x+6 =(x+6)(x+1)

x²+4x-12=(x+6)(x-2)

the least common denominator is : (x+6).......( answer: B)