Question

Find the probability of selecting none of the correct six integers in a lottery, where the order in which these integers are selected does not matter, from the positive integers not exceeding the given integers.

Answer 1

Complete Questions:

Find the probability of selecting none of the correct six integers in a lottery, where the order in which these integers are selected does not matter, from the positive integers not exceeding the given integers.

a. 40

b. 48

c. 56

d. 64

Answer:

a. 0.35

b. 0.43

c. 0.49

d. 0.54

Explanation:

(a)

The objective is to find the probability of selecting none of the correct six integers from the positive integers not exceeding 40.

Let s be the sample space of all integer not exceeding 40.

The total number of ways to select 6 numbers from 40 is
`|S| = C(40,6)`.

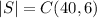Let E be the event of selecting none of the correct six integers.

The total number of ways to select the 6 incorrect numbers from 34 numbers is:

`|E| = C(34,6)`

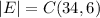
Thus, the probability of selecting none of the correct six integers, when the order in which they are selected does rot matter is

`P(E) = (|E|)/(|S|)`

`= (C(34, 6))/(C(40, 6))\\\\= (1344904)/(3838380)\\\\=0.35`

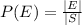
Therefore, the probability is 0.35

Check the attached files for additionals