The diameter of the tank is 24.80 ft
Explanation:
Given-
- A spherical tank holds 8,000 ft^3 of water
i.e. The volume of spherical tank = 8,000 ft^3
Now, the formula for finding volume of any spherical figure is-
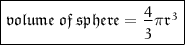
Therefore, substituting value, we get
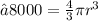
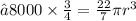
Transposing 4/3 to left hand side ,it will become 3/4 . And Here, 8000 will get cancelled by 4 leaving 2000
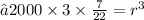
Similarly , On performing further calculations, we get. ..
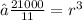
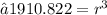
![⇢ \sqrt[3]{1910.822} = r](https://img.qammunity.org/2023/formulas/mathematics/high-school/moaurb0h50qykezoep5j19bie25x6k9mse.png)
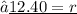
Thus, the radius of the tank is 12.40 ft
Now,
The diameter of the tank = 2 × radius
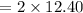
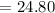
•°• The diameter of the tank comes out 24.80 ft