Question

Find the positive base $b$ in which the equation $5_b \cdot 23_b = 151_b$ is valid.

Answer 1

b=7

Explanation:

We want to determine the positive base b in which:

`5_b \cdot 23_b = 151_b`

The easiest way to approach this is to convert all the numbers to base 10.

`5_b=5Xb^0=5\\23_b =(2Xb^1)+(3Xb^0)=2b+3\\151_b=(1Xb^2)+(5Xb^1)+(1Xb^0)=b^2+5b+1\\Therefore:\\5_b \cdot 23_b = 151_b\\5(2b+3)=b^2+5b+1\\10b+15=b^2+5b+1\\b^2+5b+1-10b-15=0`

`b^2-5b-14=0`

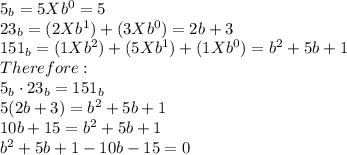
Next, we factorize the resulting expression.

`b^2-5b-14=b^2-7b+2b-14=0\\b(b-7)+2(b-7)=0\\(b-7)(b+2)=0\\b-7=0\: or \: b+2=0\\b=7\: or \: b=-2`

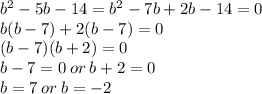
The positive value of b for which the equality hold is 7.