Question

When studying radioactive​ material, a nuclear engineer found that over 365​ days, 1,000,000 radioactive atoms decayed to 972 comma 737 radioactive​ atoms, so 27 comma 263 atoms decayed during 365 days.

a. Find the mean number of radioactive atoms that decayed in a day.

b. Find the probability that on a given​ day, 51 radioactive atoms decayed.

Answer 1

a) 74.69

b) 0.08% probability that on a given​ day, 51 radioactive atoms decayed.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

a. Find the mean number of radioactive atoms that decayed in a day.

27,263 atoms in 365 days. The mean is

`\mu = (27263)/(365) = 74.69`

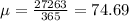
b. Find the probability that on a given​ day, 51 radioactive atoms decayed.

This is P(X = 51).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = x) = (e^(-74.69)*(74.69)^(51))/((51)!) = 0.0008`

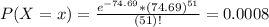
0.08% probability that on a given​ day, 51 radioactive atoms decayed.