Question

Light with a wavelength range of 141–295 nm shines on a silicon surface in a photoelectric effect apparatus, and a reversing potential of 3.50 V is applied to the resulting photoelectron.

What is the longest wavelength of the light that will eject electrons from the silicon surface?
With what maximum kinetic energy will electrons reach the anode?

Answer 1

a) the longest wavelength of the light that will eject electrons from the silicon surface is 258.7891 nm

b) maximum kinetic energy will electrons reach the anode is 0.5098 eV

Step-by-step explanation:

Given:

Wavelength range = 141-295 nm

Potential of 3.5 V

For the silicon, the work function is Φ = 4.8 eV = 7.68x10⁻¹⁹J

Questions:

a) What is the longest wavelength of the light that will eject electrons from the silicon surface, λ = ?

b) With what maximum kinetic energy will electrons reach the anode,

a) The longest wavelength that will eject electrons:

`\lambda =(hc)/(\phi )`

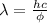
Here

h = Planck's constant = 6.625x10⁻³⁴J s

c = speed of light = 3x10⁸m/s

Substituting values:

`\lambda =(6.625x10^(-34)*3x10^(8) )/(7.68x10^(-19) ) =2.588x10^(-7) m=258.7891nm`

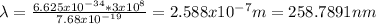
b) The maximum kinetic energy (one electron):

`K=(hc)/(\lambda ) -\phi =(6.625x10^(-34)*3x10^(8) )/(141x10^(-9) ) -7.68x10^(-19) =6.416x10^(-19) J=4.0098eV`

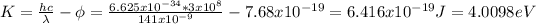
Now, you need to calculate the potential difference:

`K'=eV`

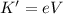
Here

e = charge of electron = 1.6x10⁻¹⁹C

Substituting:

`K'=1.6x10^(-19) *3.5=5.6x10^(-19) J=3.5eV`

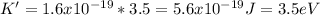
Now, the maximum kinetic energy of the electrons:

Kmax = 4.0098 - 3.5 = 0.5098 eV