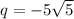Answer:
None of the options are correct
Explanation:
Given
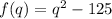
Required
The roots of the function
Since the function is a quadratic function; to get the roots of the function, f(q) must be equal to 0
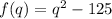 becomes
becomes
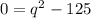
Make
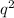 the subject of formula
the subject of formula
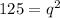
Rearrange
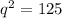
Take square roots of both sides
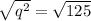
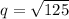
Expand the square root of 125
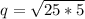
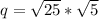
q = ±5
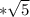
Split into 2
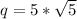 or
or
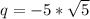
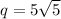 or
or
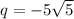
Hence, the roots of the quadratic function are
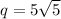 or
or