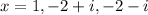Answer:
Explanation:
We are given that:
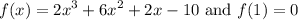
And we want to find all zeros of f algebraically.
Since f(1) = 0, then (x - 1) is a zero of f.
We can hence factor by synthetic division:
![\begin{table}[]\begin{tabular}{lllll}\multicolumn{1}l{1} & 2 & 6 & 2 & -10 \\\multicolumn{1}l{} & & 6 & 2 & 10 \\ \cline{2-5} & 2 & 8 & 10 & -10 \\ & & & & \end{tabular}\end{table}](https://img.qammunity.org/2023/formulas/mathematics/high-school/j25ty5tjvqavyurxx056f3wtheelljmtiz.png)

Therefore:
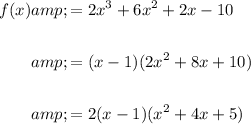
Therefore, by the Zero Product Property:
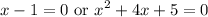
From the quadratic formula:
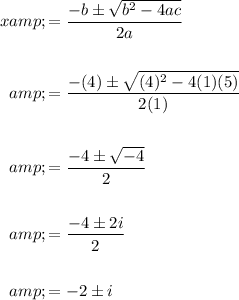
Therefore, all the zeros of f include: