Question

From a point along a straight road, the angle of elevation to the top of a hill is . From farther down the road, the angle of elevation to the top of the hill is . How high is the hill?

Answer 1

Complete Question:

From a point along a straight road, the angle of elevation to the top of a hill is 33° . A distance of 200 ft farther down the road, the angle of elevation to the top of the hill is 20°. How high is the hill?

Answer:

The hill is 165.87 ft high

Explanation:

Check the file attached below for a pictorial understanding of the question

`tan \theta = (opposite)/(Adjacent)`

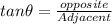
From ΔABC

`tan 33 = (y)/(x) \\`

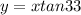`y = x tan 33`..........(1)

From ΔABD

`tan 20 = (y)/(x + 200) \\`

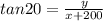
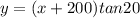`y = (x + 200) tan 20`............(2)

Equating (1) and (2)

`x tan 33 = (x+200) tan20\\xtan33 = xtan20 + 200tan20\\0.649x = 0.364x + 72.794\\0.649x - 0.364x = 72.794\\0.285x = 72.794\\x = 72.794/0.285\\x = 255.42 ft`

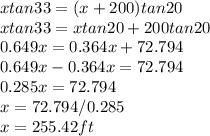
Substitute the value of x into equation (1)

`y = 255.42 tan 33`

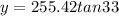
y = 165.87 ft