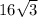Question

What is the volume of the pyramid?

12StartRoot 3 EndRoot cm3
16StartRoot 3 EndRoot cm3
24StartRoot 3 EndRoot cm3
32StartRoot 3 EndRoot cm3

Answer 1

`16√(3)`
`cm^(3)`

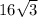
Explanation:

I think your question missed key information, allow me to add in and hope it will fit the orginal one. Please have a look at the attached photo,

A solid oblique pyramid has an equilateral triangle as a base with an edge length of 4StartRoot 3 EndRoot cm and an area of 12StartRoot 3 EndRoot cm2.

What is the volume of the pyramid?

My answer:

As we know, The volume of a pyramid =
`(1)/(3)`base area × its height

Given:

• Side lenght of the base is;
  `4√(3) cm`

=> The area of the base is
`12√(3)`
`cm^(2)`

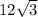
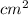
• In Δ ACB measure of angle ACB is 90° and m∠ CAB is 30°

We use:
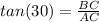
`tan(30) = (BC)/(AC)`

<=> BC =
`4√(3)*tan(30)`

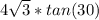
= 4 cm

And BC is the height of the the pyramid

=> The volume of a pyramid =
`(1)/(3)`
`12√(3)`
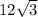
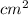`cm^(2)` * 4 cm

=
`16√(3)`
`cm^(3)`