Question

Glucose (C6H12O6)(C6H12O6) can be fermented to yield ethanol (CH3CH2OH)(CH3CH2OH) and carbon dioxide (CO2).

C6H12O6⟶2CH3CH2OH+2CO2

The molar mass of glucose is 180.15 g/mol,180.15 g/mol, the molar mass of ethanol is 46.08 g/mol,46.08 g/mol, and the molar mass of carbon dioxide is 44.01 g/mol.

a) What is the theoretical yield (in grams) of ethanol from the fermentation of 97.5 g of glucose?

b) If the reaction produced 23.4 g of ethanol, what was the percent yield?

Answer 1

Answer: a) 49.8 gram

b) 47.0 %

Step-by-step explanation:

First we have to calculate the moles of glucose

`\text{Moles of glucose}=\frac{\text{Mass of glucose}}{\text{Molar mass of glucose}}=(97.5g)/(180.15g/mole)=0.54moles`

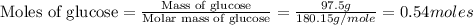
The balanced chemical reaction will be,

`C_6H_(12)O_6\rightarrow 2CH_3CH_2OH+2CO_2`

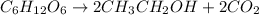
From the balanced reaction, we conclude that

As,1 mole of glucose produce = 2 moles of ethanol

So, 0.54 moles of glucose will produce =
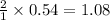`(2)/(1)* 0.54=1.08` mole of ethanol

Now we have to calculate the mass of ethanol produced

`\text{Mass of ethanol}=\text{Moles of ethanol}* \text{Molar mass of ethanol}`

`\text{Mass of ethanol}=(1.08mole)* (46.08g/mole)=49.8g`

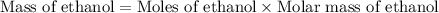
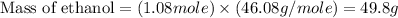
Now we have to calculate the percent yield of ethanol

`\%\text{ yield of ethanol}=\frac{\text{Actual yield}}{\text{Theoretical yield }}* 100=(23.4g)/(49.8g)* 100=47.0\%`

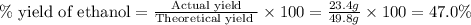
Therefore, the percent yield is 47.0 %