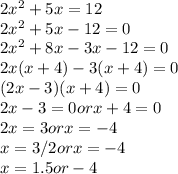Question

A student solved a quadratic equation as shown here:

2x^2+5x=12

x(2x+5)=12

x=12 or 2x+5=12

x=12 or 2x+5-5=12-5

x=12 or 2x=7

x=7/2,12

Explain the errors in the process. then correct the errors, and solve the equation.

Answer 1

x = -4, 3/2

Explanation:

Answer 2

x = 3/2 or x = -4

Explanation:

The identifiable error the students have is that before the left hand side of the equation is factorized, the right hand side value of 12 ought to be brought to the left hand side, leaving a net value of zero on the right hand side. Then whatever is factored on the left hand side is then equated to zero and then we can find the two values of x after setting each of the individual factors to zero

We proceed as follows;

`2x^(2) + 5x = 12\\2x^(2) + 5x - 12 = 0\\2x^(2) + 8x -3x -12 = 0\\2x(x+4) -3(x+4) = 0\\(2x-3)(x+4) = 0\\2x-3 = 0 or x+4 =0\\2x=3 or x=-4\\x = 3/2 or x= -4\\x = 1.5 or- 4`