Question

FIND THE RADIUS OF THE SHPERE WITH THE GIVEN VOLUME?
562.5π in.³

Answer 1

• Radius = 7.5 in

Explanation:

In the question we have given volume of Sphere that is 562.5 π in³ and we have asked to find the radius of given sphere. We know that the volume of sphere ,

`\blue{ \boxed{ \rm{Volume \: of \: Sphere = (4)/(3) \pi r {}^(3) }}}`

So equating it with given volume for finding the radius of sphere :

`\longmapsto \: (4)/(3) \pi r{}^(3) = 562.5\pi`

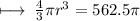
Step 1 : Cancelling π as it was present in both side :

`\longmapsto\:(4)/(3) \cancel{\pi }r{}^(3) = 562.5 \cancel{\pi}`

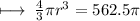
Step 2 : Transposing 4/3 to right hand side :

`\longmapsto \: r {}^(3) = 562.5 * (3)/(4)`

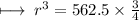
Step 3 : Multiplying 562.5 with 3 :

`\longmapsto \:r {}^(3) = (1687.5)/(4)`

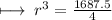
Step 4 : Dividing 1687.5 by 4 :

`\longmapsto \:r {}^(3) = 421.875`

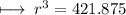
Step 5 : Finding cube root of 421.875

`\longmapsto \:r = \sqrt[3]{421.875}`

Step 6 : We get :

`\longmapsto \: \red{ \boxed{r = 7.5}}`

• Therefore , radius of sphere is 7.5 inches .

#Keep Learning