Question

A 1.30-m string of weight 0.0125 N is tied to the ceiling at its upper end, and the lower end supports a weight W. Neglect the very small variation in tension along the length of the string that is produced by the weight of the string. When you pluck the string slightly, the waves traveling up the string obey the equationy(x,t)=(8.50mm)cos(172rad⋅m−1x−2730rad⋅s−1t)Assume that the tension of the string is constant and equal to W.How much time does it take a pulse to travel the full length of the string?What was the weight W?How many wavelengths are on the string at any instant of time?What is the equation for waves traveling down the string?

Answer 1

1. t = 0.0819s

2. W = 0.25N

3. n = 36

4. y(x , t)= Acos[172x + 2730t]

Step-by-step explanation:

1) The given equation is

`y(x, t) = Acos(kx -wt)`

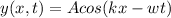
The relationship between velocity and propagation constant is

`v = (\omega)/(k)=(2730rad/sec)/(172rad/m)\\\\`

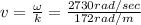
v = 15.87m/s

Time taken,
`t = (\lambda)/(v)`

`= (1.3)/(15.87)\\\\=0.0819 sec`

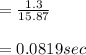
t = 0.0819s

2)

The velocity of transverse wave is given by

`v = \sqrt{(T)/(\mu)}`

`v = \sqrt{(W)/((m)/(\lambda))}`

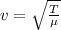
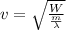
mass of string is calculated thus

mg = 0.0125N

`m = (0.0125N)/(9.8N/s)`

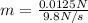
m = 0.00128kg

`\omega = (v^2m)/(\lambda)`

`\omega = ((15.87^2)(0.00128))/(1.30)`

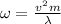
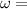`\omega =` 0.25N

3)

The propagation constant k is

`k=(2\pi)/(\lambda)`

hence

`\lambda = (2\pi)/(k)\\\\\lambda = (2 * 3.142)/(172)`

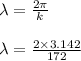
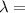`\lambda =` 0.036 m

No of wavelengths, n is

`n = (L)/(\lambda)\\\\n = (1.30m)/(0.036m)\\`

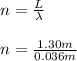
n = 36

4)

The equation of wave travelling down the string is

`y(x, t)=Acos[kx -wt]\\\\becomes\\\\y(x , t)= Acos[(172 rad.m)x + (2730 rad.s)t]`

`without, unit\\\\y(x , t)= Acos[172x + 2730t]`