Question

Determine o período e o conjunto imagem, construindo o gráfico de um período completo para cada função dada.a) por f(x) = 1+ 4 sen x.b) por f(x) = 2sen (x-3)

Answer 1

The given functions are

`f(x)=1+4sinx`

`f(x)=2sin(x-3)`

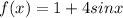
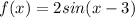
The sine function has a standard period of
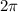`2 \pi` by definition. However, this might change if we use a factor as coefficient of the x-varible, but in this case we don't have that.

Therefore, the period of both trigonometric functions is
`2 \pi`.

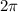Now, the images of each function is the y-variable set values that defines each function.

So, the function
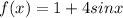`f(x)=1+4sinx` has an image defined by the set
`[-3,5]`. It's impotant to notice that the range of a standard function is [-1,1], however, in this case, the function was shifted 1 unit up and it was streched by a factor of 4, that's why the standard image changes to
`[-3,5]`.

About the second function
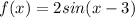`f(x)=2sin(x-3)`, the image set is
`[-2,2]`, because the function was streched by a factor of 2.

Additionally, the image attached shows the graph of the given functions.