Answer:
1/6
Step-by-step explanation:
The circumference of a circle is denoted by:
 , where r is the radius. Here, r = 1, so plug this in:
, where r is the radius. Here, r = 1, so plug this in:

 units
units
Now, we know that arc AB has a length of
 and we want to find the fraction of the circumference this is. So, divide
and we want to find the fraction of the circumference this is. So, divide
 by
by
 :
:
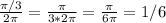
Thus, the fraction is 1/6.
Hope this helps!