Answer:
(1) The maximum air temperature is 1383.002 K
(2) The rate of heat addition is 215.5 kW
Step-by-step explanation:
T₁ = 17 + 273.15 = 290.15
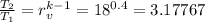
T₂ = 290.15 × 3.17767 = 922.00139
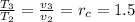
Therefore,
T₃ = T₂×1.5 = 922.00139 × 1.5 = 1383.002 K
The maximum air temperature = T₃ = 1383.002 K
(2)
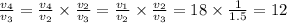
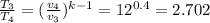
Therefore;
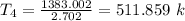
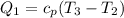
Q₁ = 1.005(1383.002 - 922.00139) = 463.306 kJ/jg
Heat rejected per kilogram is given by the following relation;
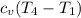 = 0.718×(511.859 - 290.15) = 159.187 kJ/kg
= 0.718×(511.859 - 290.15) = 159.187 kJ/kg
The efficiency is given by the following relation;
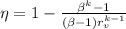
Where:
β = Cut off ratio
Plugging in the values, we get;
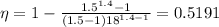
Therefore;
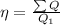
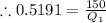
Heat supplied =

Therefore, heat supplied = 215491.064 W
Heat supplied ≈ 215.5 kW
The rate of heat addition = 215.5 kW.