Question

Steve wants to know what the average ACT scores of students graduated from his high school is. He randomly selected 25 students from an email list and asked them to provide the information. Of them 20 students replied and the summary of the ACT score is as below. Steve is told that the population standard deviation for ACT score is 4.6 for his high school, estimate the population average ACT score of his high school graduates with 86% confidence level. Sample size Mean STD Min Max 20 21.5 5.7 15 26 What is the appropriate inference procedure we need to use to answer the research question?

Answer 1

The 86% confidence interval for the population mean is (19.982, 23.018).

As we are using a sample to make an inference about the population mean, we use a confidence interval with a certain degree of confidence.

We are 86% confident that the true mean ACT scores is between 19.982 and 23.018.

Explanation:

We have the information:

Sample size n= 20

Mean M=21.5

STD s=5.7

Min = 15

Max = 26

Population STD σ=4.6

Confidence level = 86%

We have to calculate a 86% confidence interval for the mean.

The population standard deviation is know and is σ=4.6.

The sample mean is M=21.5.

The sample size is N=20.

As σ is known, the standard error of the mean (σM) is calculated as:

`\sigma_M=(\sigma)/(√(N))=(4.6)/(√(20))=(4.6)/(4.4721)=1.0286`

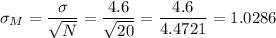
The t-value for a 86% confidence interval is z=1.476.

The margin of error (MOE) can be calculated as:

`MOE=z\cdot \sigma_M=1.476 \cdot 1.0286=1.518`

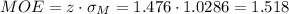
Then, the lower and upper bounds of the confidence interval are:

`LL=M-t \cdot s_M = 21.5-1.518=19.982\\\\UL=M+t \cdot s_M = 21.5+1.518=23.018`

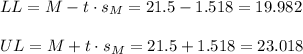
The 86% confidence interval for the population mean is (19.982, 23.018).

As we are using a sample to make an inference about the population mean, we use a confidence interval with a certain degree of confidence.

We are 86% confident that the true mean ACT scores is between 19.98 and 23.02.