Question

A survey found that 39% of the population owned dogs, 22% owned

cats, and 8% of the population owned both a cat and a dog? Find
the probability that a person owns a cat or a dog.

Answer 1

0.53

Explanation:

Percentage who owned dogs, n(D)=39%

Percentage who owned cats, n(C)=22%

Percentage who owned both dogs and cats,
`n(C\cap D)=8\%`

From Probability Theory

`P(C\cup D)=P(C)+P(D)-P(C\cap D)\\=0.22+0.39-0.08\\P(C\cup D)=0.53`

The probability that a person owns a cat or a dog therefore is 0.53.

Answer 2

53% probability that a person owns a cat or a dog.

Explanation:

I am going to solve this question building the Venn's diagram of these probabilities,

We have that:

P(A) is the probability that a person owns a dog.

P(B) is the probability that a person owns a cat.

8% of the population owned both a cat and a dog

This means that
`P(A \cap B) = 0.08`

22% owned cats

This means that
`P(B) = 0.22`

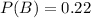
39% of the population owned dogs

This means that
`P(A) = 0.39`

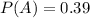
Find the probability that a person owns a cat or a dog.

This is
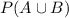`P(A \cup B)`, which is given by:

`P(A \cup B) = P(A) + P(B) - P(A \cap B)`

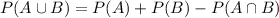
So

`P(A \cup B) = 0.39 + 0.22 - 0.08 = 0.53`

53% probability that a person owns a cat or a dog.