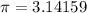Question

Victor measured a circular lid and found d, the diameter, was 8 inches and C, the circumference was 25 inches. Which expression represents an approximate value for π

Answer 1

25/8

Explanation:

I had the same question sorry if im wrong

Answer 2

`r = (d)/(2)= (8)/(2)= 4`

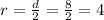
And we also know that circumference C =25 inches and the formula for this circumference is given by:

`C = 2\pi r`

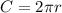
We want to find the value of
`\pi` and solving from the last equation we got:

`\pi = (C)/(2r)`

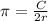
And replacing we got:

`\pi = (25)/(2*4)= 3.125`

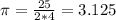
So then the approximation for the value of
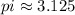`pi \approx 3.125` and that's very close to the real value of
`\pi = 3.14159`

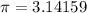
Explanation:

For this case we know that the diameter d =8 in. And we can find the radius from this info since d = 2r with r representing the radius. If we solve for r we got:

`r = (d)/(2)= (8)/(2)= 4`

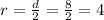
And we also know that circumference C =25 inches and the formula for this circumference is given by:

`C = 2\pi r`

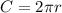
We want to find the value of
`\pi` and solving from the last equation we got:

`\pi = (C)/(2r)`

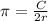
And replacing we got:

`\pi = (25)/(2*4)= 3.125`

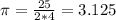
So then the approximation for the value of
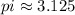`pi \approx 3.125` and that's very close to the real value of
`\pi = 3.14159`