Question

The value of a particular investment follows a pattern of exponential growth. In the year 2000, you invested money in a money market account. The value of your investment t years after 2000 is given by the exponential growth model A=1700e^0.062t When will the account be worth $2466?

Answer 1

The value of the investment will be worth $2466 in the year 2017

Explanation:

In this question, we are tasked with finding the specific year in which an amount invested in a money market account reaches a particular value

To get this year, what we need to do is to get the value of t from the exponential equation given in the question. To get t, we simply make the value of A set to the particular value in the question.

Hence, we use
`A = 1700e^(0.062t) \\`

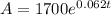
Now, we plug the value of A = 2466 and take the natural logarithm of both sides i.e
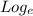`Log_(e)` or simply ln

From;

`2466 = 1700e^(0.062t)`

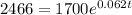
ln 2466 = ln
`1700e^(0.062t)`

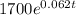
ln 2466 = 0.062t ln1700

7.81 = 0.062t × 7.44

t = 7.81/(0.062 × 7.44)

t = 16.93 approximately 17 years

This means that the value of the investment will have that worth in the year 2000+17 = year 2017