Answer:
The correct option is (D).
Explanation:
To construct the (1 - α)% confidence interval for population proportion the distribution of proportions must be approximated by the normal distribution.
A Normal approximation to binomial can be applied to approximate the distribution of proportion p, if the following conditions are satisfied:
In this case p is defined as the proportions of students who ride a bike to campus.
A sample of n = 125 students are selected. Of these 125 students X = 6 ride a bike to campus.
Compute the sample proportion as follows:

Check whether the conditions of Normal approximation are satisfied:
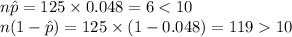
Since
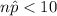 , the Normal approximation to Binomial cannot be applied.
, the Normal approximation to Binomial cannot be applied.
Thus, the confidence interval cannot be used to estimate the proportion of all students who ride a bike to campus.
Thus, the correct option is (D).