Answer:
a
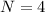
b
The standard deviation is
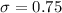
c
The uncertainty at 95% is
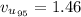
d
The interval about the sample mean is

Step-by-step explanation:
From the question we are told that
The confidence level is
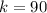 %
%
The mean velocity is
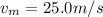
The velocity standard deviation is
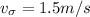
The uncertainty of the velocity
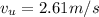
Generally uncertainty can be represented mathematically as
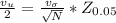
Where
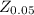 is the z-score of 0,05 = 1.645 from the z-table
is the z-score of 0,05 = 1.645 from the z-table
Substituting value
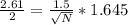

The standard deviation of the mean is mathematically represented as

Substituting the values
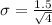
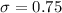
The uncertainty for confidence level of 95% is mathematically represented as
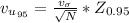
Where
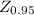 is the z value of the 0.95 which is 1.96, this is obtained using the z-table
is the z value of the 0.95 which is 1.96, this is obtained using the z-table
Substituting values
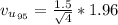
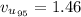
The uncertainty for confidence level of 50 % is mathematically represented as

Where
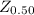 is the z value of the 0.50 which is 0.69146, this is obtained using the z-table
is the z value of the 0.50 which is 0.69146, this is obtained using the z-table
Substituting values
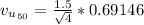
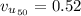
So the interval about the sample mean is
