Question

A cake has two layers. Each layer is a regular hexagonal prism. You cut and remove a slice that takes away one face of each prism as shown. What is the volume of the​ slice? What is the volume of the remaining​ cake? Use pencil and paper. Describe two ways to find the volume of the slice.

Answer 1

The volume of slice is 142

The volume of the remaining cake is 708

Step-by-step explanation:

Answer 2

Volume of slice is approximately 40 in³

Volume of the remaining cake is 197.014 in³

Step-by-step explanation:

Here we have two regular hexagons

one top small hexagon cake with side length = 3 in, height = 3 in

One big hexagon cake, side length = 4 in, Height = 4 in

A slice cut such the it removes a side segment is equivalent to an equilateral triangle with side length = length of hexagon side

Also all angles within the equilateral triangle are 60° each

Therefore, the length of the side of the removed equilateral triangle side is given as follows;

Top small cake slice triangle side = 3 in.

Area of surface of small slice =
`(1)/(2) * Base * Height = (1)/(2) * 3 * 3* sin(60) = (1)/(2) * 3 * 3 * (√(3) )/(2) = (9√(3) )/(4)`

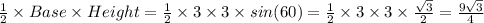
Volume of small slice = Area of surface small slice × Height of small cake

=
`(9√(3) )/(4) * 3 = (27√(3) )/(4) =11.69 \ in^3 \approx 12 \ in^3`

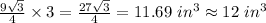
For the big cake, we have;

Big cake slice triangle side = 4 in.

Area of surface of big slice =
`(1)/(2) * Base * Height = (1)/(2) * 4 * 4* sin(60) = 8 * (√(3) )/(2) = 4√(3)`

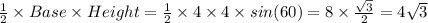
Volume of big slice = Area of surface of big slice × Height of big slice

=
`4√(3) * 4 = 16√(3) =27.71 \ in^3 \approx 28 \ in^3`

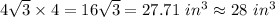
Total volume of slice = Volume of small slice + Volume of big slice

Total volume of slice = 12 in³ +28 in³ = 40 in³

The volume of the remaining cake can be found by noting that there were 6 possible slices of cake based on the 6 sides of the hexagon, since we removed 1 slice, the remaining 5 slices will have a volume given by multiplying the volume of 1 slice by 5 as follows;

For the small cake, the remaining volume =
`5 * (27√(3) )/(4) = 5 * 11.69 \ in^3 = 58.45 \ in^3`

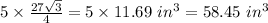
For the big cake the remaining volume =
`5 * 16√(3) = 5 * 27.71 \ in^3 = 138.56 \ in^3`

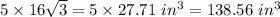
Total volume remaining cake = 58.45 in³ + 138.56 in³ = 197.014 in³

Together with the above way to find the volume of slice of cake, the volume of the slice can also be found by considering that the cake, with a shape of a regular hexagon is made up of 6 such slices. Therefore, if the volume of a regular hexagon is as follows;

`Volume\, of \, regular \, hexagon, \ A = (3√(3) )/(2) a^2 * h`

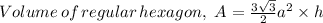
Where:

a = Length of side

h = Height of hexagon

The volume of each slice is therefore,

`(Volume\, of \, regular \, hexagon, \ A )/(6) =( (3√(3) )/(2) a^2 * h)/(6) = a^2 * h * (3√(3) )/(12) = a^2 * h * (√(3) )/(4)`

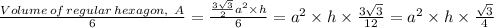
For the small cake, we have

a = 3 in.

h = 3 in.

Volume of small slice =
`a^2 * h * (√(3) )/(4) = (3^2√(3) )/(4) * 3 = (27√(3) )/(4) \ in^3`.

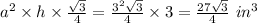For the big cake, we have

a = 4 in.

h = 4 in.

Volume of big slice =
`a^2 * h * (√(3) )/(4) = (4^2√(3) )/(4) * 4 = 16√(3) \ in^3`.

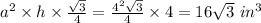Total volume of slice = Volume of small slice + Volume of big slice

Total volume of slice =
`(27√(3) )/(4) \ in^3 +16√(3) \ in^3 = (91√(3) )/(4) \ in^3 = 39.404 \ in^3`

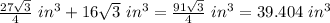
Total volume of slice = 39404 in³.