Answer:
Explanation:
The matrix is
![\left[\begin{matrix}1 & -2 & 3\\ -1 & 3 & -4 \\ -5&-2 & 9\end{matrix}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/m0il25mgnmaax1xrvd1ee6an3w63l8daaw.png)
Since this matrix represents a transformation, for us to check if it maps
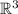 onto
onto
There is a theorem as a follows: A linear transformation is one to one if and only if the kernel of it's matrix representation is the vector 0. Recall that given a matrix A the kernel is defined as
KerA =
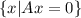
which is equivalent to solve the homogeneous system, and finding that the only solution is the vector 0. We will solve the system by gauss-jordan reduction.
If we apply gauss -jordan reduction to the matrix A, we get (the calculations of this matrix are beyond the scope of this answer)
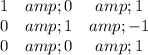
If we translate this to a equations system we get
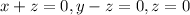
We have that x=-z, y=z and z=0. Which shows that the only solution is the vector (0,0,0).
Hence, T is a one- to-one transformation. To check that T is a onto transformation, we only need to check that the reduced form of the matrix has the same number of pivots as the dimension of the codomain (in this case, R^3). Since
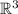 is a 3-dimensional vector space, the reduced matrix must have 3 pivots. So, since the matrix is 3x3 matrix, each column must have a pivot.
is a 3-dimensional vector space, the reduced matrix must have 3 pivots. So, since the matrix is 3x3 matrix, each column must have a pivot.
One can identify a pivot if it's a non zero entry whose entries that are on the same row and at the left, and all the entries of the same column that are under the entry are all 0.
We can check that in this case each column has the pivot 1 at columns 1, 2, and 3. So, since the reduced form has 3 pivots, T maps
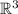 onto
onto