Question

A soccer ball was kicked in the air and follows the path h(x)=−2x2+1x+6, where x is the time in seconds and h is the height of the soccer ball. At what time will the soccer ball hit the ground?

Answer 1

Explanation:

The soccer ball was kicked in the air and follows the path as :

`h(x)=-2x^2+x+6`

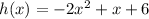
Here, x is the time in seconds and h is the height of the soccer ball.

We need to find the time at which the soccer ball hit the ground. It means that its height at a function of time becomes 0. So,

h(x) = 0

`-2x^2+x+6=0\\\\2x^2-x-6=0`

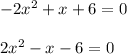
The above equation is a quadratic equation. It can be calculated as :

`x= \frac{-b \pm \sqrt{b^(2) - 4ac } }{2a}\\\\x= \frac{-b + \sqrt{b^(2) - 4ac } }{2a},x= \frac{-b - \sqrt{b^(2) - 4ac } }{2}\\\\x= \frac{-(-1) + \sqrt{(-1)^(2) - 4(2)(-6) } }{2(2)},x= \frac{-(-1) - \sqrt{(-1)^(2) - 4(2)(-6) } }{2(2)}\\\\x=2,-1.5`

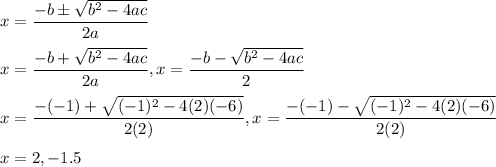
So, at 2 seconds the ball will hit the ground.