Question

The Internal Revenue Service (IRS) provides a toll-free help line for taxpayers to call in and get answers to questions as they prepare their tax returns. In recent years, the IRS has been inundated with taxpayer calls and has redesigned its phone service as well as posting answers to frequently asked questions on its website (The Cincinnati Enquirer, January 7, 2010). According to a report by a taxpayer advocate, callers using the new system can expect to wait on hold for an unreasonably long time of 14 minutes before being able to talk to an IRS employee. Suppose you select a sample of 50 callers after the new phone service has been implemented; the sample results show a mean waiting time of 12 minutes before an IRS employee comes on line. Based upon data from past years, you decide it is reasonable to assume that the standard deviation of waiting times is 10 minutes. Using your sample results, can you conclude that the actual mean waiting time turned out to be significantly less than the 14-minute claim made by the taxpayer advocate? Use α = .05.

a. State the hypotheses.
H0: μ - Select your answer -greater than or equal to 14less than or equal to 14less than 14
Ha: μ - Select your answer -more than 14greater than or equal to 14less than 14

b. What is the p-value (to 4 decimals)?

c. Using α = .05, can you conclude that the actual mean waiting time is significantly less than the claim of 14 minutes made by the taxpayer advocate.
- Select your answer -YesNo

Answer 1

ame here lookig for

Explanation:

Decide if the answer to 8/8 x 10 is less than, greater than, or equal to 10.

instead got

The Internal Revenue Service (IRS) provides a toll-free help line for taxpayers to call in and get answers to questions as they prepare their tax returns. In recent years, the IRS has been inundated with taxpayer calls and has redesigned its phone service as well as posting answers to frequently asked questions on its website (The Cincinnati Enquirer, January 7, 2010). According to a report by a taxpayer advocate, callers using the new system can expect to wait on hold for an unreasonably long time of 14 minutes before being able to talk to an IRS employee. Suppose you select a sample of 50 callers after the new phone service has been implemented; the sample results show a mean waiting time of 12 minutes before an IRS employee comes on line. Based upon data from past years, you decide it is reasonable to assume that the standard deviation of waiting times is 10 minutes. Using your sample results, can you conclude that the actual mean waiting time turned out to be significantly less than the 14-minute claim made by the taxpayer advocate? Use α = .05. a. State the hypotheses. H0: μ - Select your answer -greater than or equal to 14less than or equal to 14less than 14 Ha: μ - Select your answer -more than 14greater than or equal to 14less than 14 b. What is the p-value (to 4 decimals)? c. Using α = .05, can you conclude that the actual mean waiting time is significantly less than the claim of 14 minutes made by the taxpayer advocate. - Select your answer -YesNo

Answer 2

a) Null hypothesis:
`\mu \geq 14`

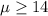
Alternative hypothesis:
`\mu < 14`

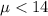
H0: μ -greater than or equal to 14

Ha: μ - less than 14

b)
`p_v =P(t_((49))<-1.414)=0.0818`

c) For this case since the p value is higher than the significance level given of 0.05 the answer would be NO

We can't conclude that the actual mean waiting time is significantly less than the claim of 14 minutes made by the taxpayer advocate

Explanation:

Data given

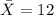`\bar X=12` represent the sample mean

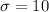`\sigma=10` represent the population standard deviation

`n=50` sample size

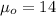`\mu_o =14` represent the value that we want to test

`\alpha=0.05` represent the significance level for the hypothesis test.

z would represent the statistic (variable of interest)

`p_v` represent the p value for the test (variable of interest)

Part a: System of hypothesis

We need to conduct a hypothesis in order to check if the true mean is less than 14 minute, the system of hypothesis would be:

Null hypothesis:
`\mu \geq 14`

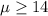
Alternative hypothesis:
`\mu < 14`

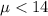
The statistic is given by:

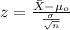`z=(\bar X-\mu_o)/((\sigma)/(√(n)))` (1)

Calculate the statistic

If we replace we got:

`t=(12-14)/((10)/(√(50)))=-1.414`

Part b: P-value

The first step is calculate the degrees of freedom, on this case:

`df=n-1=50-1=49`

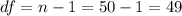
Since is a one sided lower test the p value would be:

`p_v =P(t_((49))<-1.414)=0.0818`

Part c

For this case since the p value is higher than the significance level given of 0.05 the answer would be NO

We can't conclude that the actual mean waiting time is significantly less than the claim of 14 minutes made by the taxpayer advocate