Question

If a substance decays at a rate of 25% every 10 years, how long will it take 512 grams of the substance to decay to 121.5 grams

Answer 1

It will take 50 years to decay from 512 grams to 121.5 grams.

Explanation:

The decay formula :

`N=N_0e^(-\lambda t)`

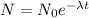
where

N= amount of substance after t time

N₀= initial of substance

t= time.

A substance decays at a rate 25% every 10 years.

So, remaining amount of the substance is = (100%-25%)= 75%

`(N)/(N_0)=(75\%)/(100\%)=(75)/(100)=\frac34`, t= 10

`N=N_0e^(-\lambda t)`

`\Rightarrow \frac {N}{N_0}=e^(-\lambda t)`

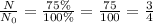`\Rightarrow \frac34 =e^(-\lambda .10)`

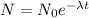
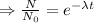
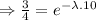
Taking ln both sides

`\Rightarrow ln|\frac34| =ln|e^(-\lambda .10)|`

`\Rightarrow ln|\frac34|=-10\lambda`

`\Rightarrow \lambda=( ln|\frac34|)/(-10)`

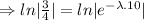
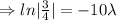
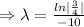
Now , N₀= 512 grams, N= 121.5 grams, t=?

`N=N_0e^(-\lambda t)`

`\therefore 121.5=512e^\frac34`

`\Rightarrow 121.5=512e^(ln`

`\Rightarrow (121.5)/(512)=e^(ln`

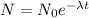
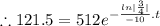
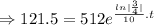
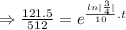
Taking ln both sides

`\Rightarrow ln|(121.5)/(512)|=ln|e^\frac34|`

`\Rightarrow ln|(121.5)/(512)|=\frac34`

`\Rightarrow t=(ln|(121.5)/(512)|)/((ln|\frac34|)/(10))`

`\Rightarrow t=\frac10.ln{ln}`

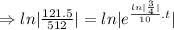
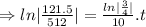
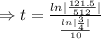
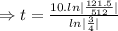
⇒t=50 years

It will take 50 years to decay from 512 grams to 121.5 grams.