Question

The uniform slender bar ABC weighs 4.3 lb and is initially at rest with end A bearing against the stop in the horizontal guide. When a constant couple M = 62.1 lb-in. is applied to end C, the bar rotates causing end A to strike the side of the vertical guide with a velocity of 11.6 ft/sec. Calculate the loss of energy ΔE (enter a positive number) due to friction in the guides and rollers. The mass of the rollers may be neglected.

Answer 1

the energy loss due to friction = 0.2344 ft-lb

Step-by-step explanation:

The principle of conservation of energy is used to calculate the loss of energy due to friction.

The difference between the gain in potential (Mθ) due to the restoring moment M = 62.1 lb-in and loss in potential energy due to weight (mgh) and kinetic energy as a result of restoration
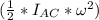`((1)/(2)*I_(AC)* \omega ^2)` of AC adds up to the energy loss ( ΔE).

Expressing the formula; we have:

ΔE =
`M \theta - mgh - (1)/(2)*I_(AC)* \omega^2`

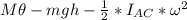
ΔE =
`M \theta - mgh - (1)/(2)*(mb^2)/(12)* ((v)/(r))^2`

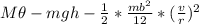
From the diagram below; the weight of the slender = W

acceleration due to gravity = g

length of the slender bar = r

the couple = M

the vertical guide velocity = v

and the angle = θ

ΔE =
`(62.1)/(12)*(\pi)/(4)-4.3*(8)/(12) *(1-(1)/(√(2)))- [(1)/(2)*((1)/(12))*(4.3)/(32.2)*((16)/(12))^2*((11.6)/((8)/(12)))^2]`

ΔE = 4.064 - 0.8396 - 2.99

ΔE = 0.2344 ft-lb

Thus, the energy loss due to friction = 0.2344 ft-lb