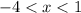Answer:
a)
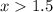
b)
Explanation:
Given that function is a third order polynomial, it can be factorized:
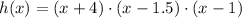
The following inequation must be analyzed to determine which sections are above sea level:
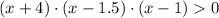
By Algebra, it is known that product between three positive numbers or two negative numbers and a positive number are equal to a positive number. Then, there are only two trails:
a)
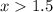
b)