Question

In a chess tournament, 10 games are being played, independently. Each game ends in a win for one player with probability 0.4 and ends in a draw (tie) with probability 0.6 . Find the probability that exactly 5 games end in a draw.

Answer 1

The probability that exactly 5 games end in a draw is 0.201.

Explanation:

The random variable X can be defined as the number of games that end in a draw.

The tournament consists of n = 10 games, being played independently.

The probability of a game ending in a draw is, p = 0.60.

A randomly selected game ending in a draw is independent of the other games.

The random variable X follows a Binomial distribution with parameters n = 10 and p = 0.60.

The probability mass function of X is:

`P(X=x)={10\choose x}\ 0.60^(x)(1-0.60)^(10-x);\ x=0,1,2,3...`

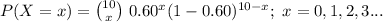
Compute the probability that exactly 5 games end in a draw as follows:

`P(X=5)={10\choose 5}\ 0.60^(5)(1-0.60)^(10-5)\\=252* 0.07776* 0.01024\\=0.2006581248\\\approx 0.201`

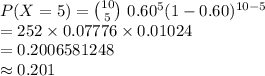
Thus, the probability that exactly 5 games end in a draw is 0.201.