Answer:
The probability that exactly 5 games end in a draw is 0.201.
Explanation:
The random variable X can be defined as the number of games that end in a draw.
The tournament consists of n = 10 games, being played independently.
The probability of a game ending in a draw is, p = 0.60.
A randomly selected game ending in a draw is independent of the other games.
The random variable X follows a Binomial distribution with parameters n = 10 and p = 0.60.
The probability mass function of X is:
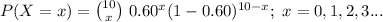
Compute the probability that exactly 5 games end in a draw as follows:
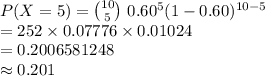
Thus, the probability that exactly 5 games end in a draw is 0.201.