Question

cost of carrying 1 unit is $1.2 per year. The shop has 360 working days per year. The lead time is usually 12 working days. Determine the annual total relevant, including ordering and carrying, cost.

Answer 1

I. Annual ordering cost = $240

II. Annual carrying cost = $240

III. Total annual inventory cost = $480

Step-by-step explanation:

We begin by listing out the data we were given, we have:

annual demand (D) = 1200, ordering cost (S) = $80 per order,

per unit cost (H) = $ 1.20, number of working days = 360 days,

lead time = 12 days

To calculate the economic order quantity we use the formula

economic order quantity = square root of [(2 * annual demand * the ordering cost) ÷ (per unit cost)]

Mathematically,

EOQ =
`√(2DS/H)`

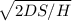
where:

D = annual demand, S = ordering cost, H = unit cost

Substite the variables into the formula, we have:

EOQ =
`√((2*1200*80)/1.2)`

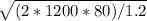
EOQ =
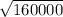`√(160000)` = 400

EOQ = 400 units

I. Annual ordering cost = annual demand * ordering cost ÷ order size

number of orders (Q) = annual demand ÷ order size = 1200/400 = 3 orders

Annual ordering cost = ordering cost * number of orders

Annual ordering cost = S * Q ⇒ 80 * 3

Annual ordering cost = $240

II. Annual carrying cost = average inventory * per unit cost

average inventory = EOQ ÷ 2

Annual carrying cost = (EOQ * H) ÷ 2

Annual carrying cost = 400 * 1.2 ÷ 2 = 240

Annual carrying cost = $240

Total annual inventory cost = Annual ordering cost + Annual carrying cost

Total annual inventory cost = $ (240 + 240)

Total annual inventory cost = $480