Answer:
(a) The probability that a person has to wait less than 6 minutes for the bus is 0.24.
(b) The probability that a person has to wait between 10 and 20 minutes for the bus is 0.40.
Explanation:
Let The random variable X be defined as the waiting time for a bus at a certain bus stop.
The random variable X follows a continuous Uniform distribution with parameters a = 0 and b = 25.
The probability density function of X is:

(a)
Compute the probability that a person has to wait less than 6 minutes for the bus as follows:
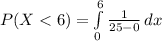
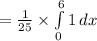
![=(1)/(25)* [x]^(6)_(0)](https://img.qammunity.org/2021/formulas/mathematics/college/o8i7zkwek8v3xm7y902jywpg4nief1k7fx.png)
![=(1)/(25)* [6-0]](https://img.qammunity.org/2021/formulas/mathematics/college/tnplmypmha8vtuy184nf4b7dsy89tdsdm4.png)
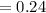
Thus, the probability that a person has to wait less than 6 minutes for the bus is 0.24.
(b)
Compute the probability that a person has to wait between 10 and 20 minutes for the bus as follows:

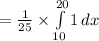
![=(1)/(25)* [x]^(20)_(10)](https://img.qammunity.org/2021/formulas/mathematics/college/72txyz8zxxpdrfkojpr4zgfvuousyn6px5.png)
![=(1)/(25)* [20-10]](https://img.qammunity.org/2021/formulas/mathematics/college/xk6w74qahvbvs301vv4fwk6bx7bope4lim.png)
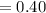
Thus, the probability that a person has to wait between 10 and 20 minutes for the bus is 0.40.