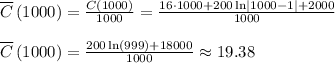Answer:
The cost function is
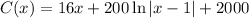 .
.
The average cost of 1000 shoes is $19.38.
Explanation:
We define the marginal cost function to be the derivative of the cost function or
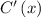 .
.
To find the cost function,
 we need to integrate the marginal cost function
we need to integrate the marginal cost function

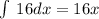
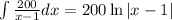

We know that the fixed costs are $2,000 per week, so the constant
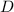 is equal to 2000, and the cost function is
is equal to 2000, and the cost function is
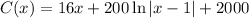
If
 is the cost function for some item then the average cost function is,
is the cost function for some item then the average cost function is,
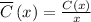
We know that 1,000 pairs of shoes are produced each week, so the the average cost is