Answer:
Below!
Explanation:
Let the irrational number be known as "x".
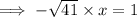
Divide both sides by -√41.
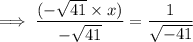
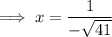
Take the "-" to the numerator:
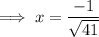
Use parenthesis to isolate the "-"
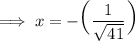
Note: 1 can also be written as √1. (√1 = √1 × √1 = 1)
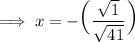
Combine the roots in the equation:
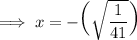
Remove the parenthesis:
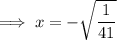
Thus, Option C is correct.