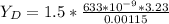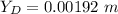Question

As an admirer of Thomas Young, you perform a double-slit experiment in his honor. You set your slits 1.15 mm apart and position your screen 3.23 m from the slits. Although Young had to struggle to achieve a monochromatic light beam of sufficient intensity, you simply turn on a laser with a wavelength of 633 nm . How far on the screen are the first bright fringe and the second dark fringe from the central bright fringe?

Answer 1

The distance of the first bright fringe is given as
`Y_C = 1.22 *10^(-3)m`

The distance of the second dark fringe from the central bright fringe is given as
`Y_D = 0.00192 \ m`

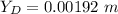
Step-by-step explanation:

From the question we are told that

The slit separation distance is
`d = 1.15 mm = (1.15)/(1000) =0.00115 m`

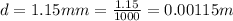
The distance of the slit from the screen is
`D = 3.23 m`

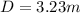
The wavelength is
`\lambda = 633 nm`

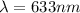
For constructive interference to occur the distance between the two slit is mathematically represented as

`Y_C =(m \lambda D)/(d)`

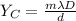
Where m is the order of the fringe which has a value of 1 for first bright fringe

Substituting values

`Y_C = (1 * 633 *0^(-9) * 3.23)/(0.00115)`

`Y_C = 1.22 *10^(-3)m`

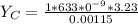
For destructive interference to occur the distance between the two slit is mathematically represented as

`Y_D = [n + (1)/(2) ] (\lambda D)/(d)`

m = 2

so the formula to get the dark fringe is
`n = (1)/(2) * 1`

`n=1`

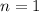
Now substituting values

`Y_D = [ 1 + (1)/(2) ] * (633 *10^(-9) * 3.23 )/(0.00115)`

`Y_D =1.5 * (633 *10^(-9) * 3.23 )/(0.00115)`

`Y_D = 0.00192 \ m`