Answer:
1) The solutions are:
smaller r = -8
larger r = -1
2) The vertex is
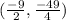 .
.
Explanation:
1) A zero of a function is an x-value that makes the function value 0.
To find the zeros of the function, first, we see that the linear factors of
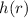 are
are
 and
and
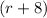 .
.
If we set
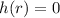 and solve for x, we get
and solve for x, we get
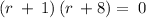
Using the Zero factor principle, If ab = 0, then either a = 0 or b = 0, or both a and b are 0.
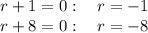
The solutions are:
smaller r = -8
larger r = -1
2) The vertex of a parabola is the highest or lowest point, also known as the maximum or minimum of a parabola.
To find the vertex of the function
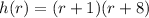 , first we need to find the standard equation of a parabola, which is,
, first we need to find the standard equation of a parabola, which is,

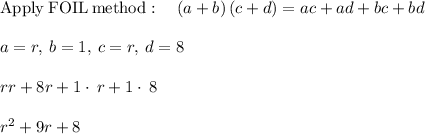
Next, we find the r-coordinate of the vertex with the formula
 .
.
We know from the standard equation of a parabola that

So,
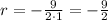
And the h-coordinate is
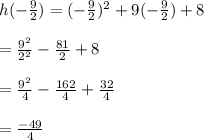
The vertex is
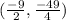 .
.