Answer:
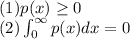
Step-by-step explanation:
A function f(x) is a Probability Density Function if it satisfies the following conditions:
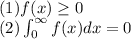
Given the function:
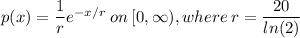
(1)p(x) is greater than zero since the range of exponents of the Euler's number will lie in
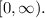
(2)
![\int_(0)^(\infty) p(x)=\int_(0)^(\infty) (1)/(r)e^(-x/r)\\=(1)/(r) \int_(0)^(\infty) e^(-x/r)\\=-(r)/(r)\left[e^(-x/r)\right]_(0)^(\infty)\\=-\left[e^(-\infty/r)-e^(-0/r)\right]\\=-e^(-\infty)+e^(-0)\\SInce \: e^(-\infty) \rightarrow 0\\e^(-0)=1\\\int_(0)^(\infty) p(x)=1](https://img.qammunity.org/2021/formulas/physics/college/kl8cueia10z2k2forsqnh0oxft0o6byvmo.png)
The function p(x) satisfies the conditions for a probability density function.